Welcome to Sudoku Today!
Welcome to Sudoku.today! Enjoy daily Sudoku puzzles including classic Sudoku and over 50 unique variants. Challenge your mind every day with new puzzles!

New Tutorial: Master Advanced Sudoku Techniques
Visualize the logic of Skyscraper, 2-String Kite, and Turbot Fish (X-Chain).
▶ Watch VideoToday's Sudoku
30 January 2026
Hybrid Sudoku ( X Sums + Greater Than )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
- Digits have to be place in accordance with the “greater than” signs.
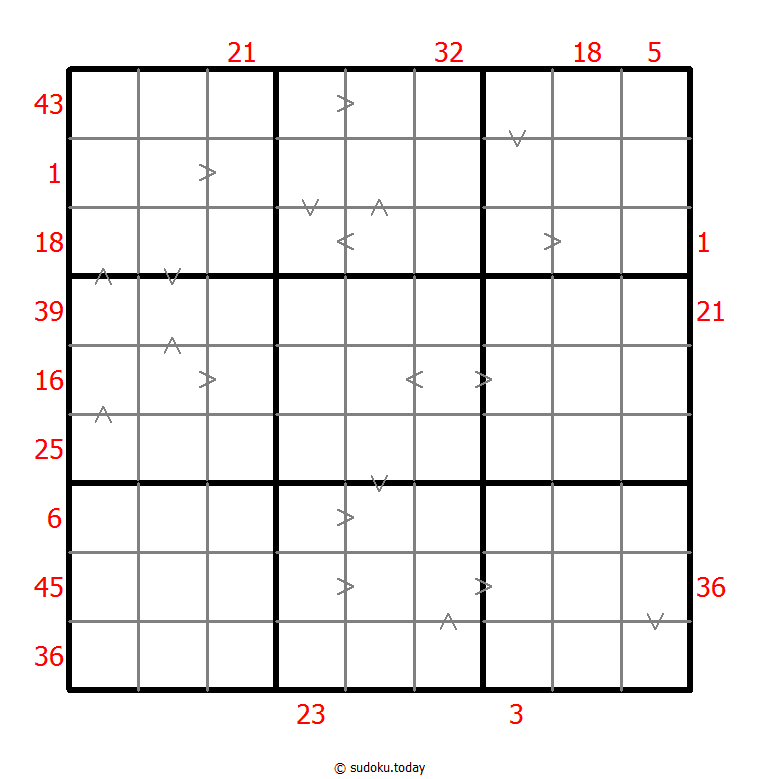
Hybrid Sudoku ( X Sums + Greater Than )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
- Digits have to be place in accordance with the “greater than” signs.
Creasing Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits along each line are monotonically increasing or decreasing.
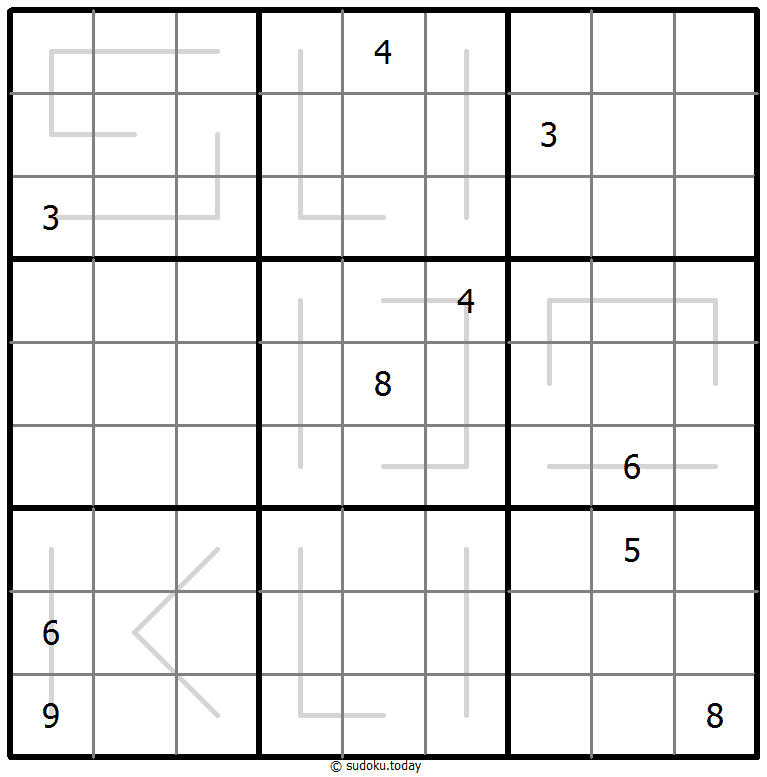
Creasing Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits along each line are monotonically increasing or decreasing.
Hybrid Sudoku ( Consecutive Pairs + Sum Frame )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
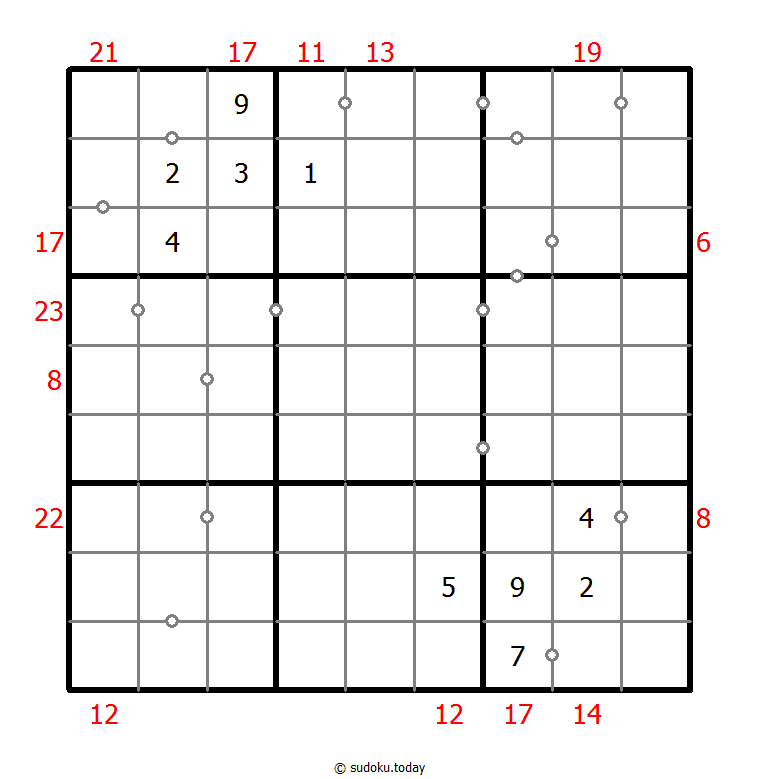
Hybrid Sudoku ( Consecutive Pairs + Sum Frame )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
Consecutive Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. All possible dots are marked.
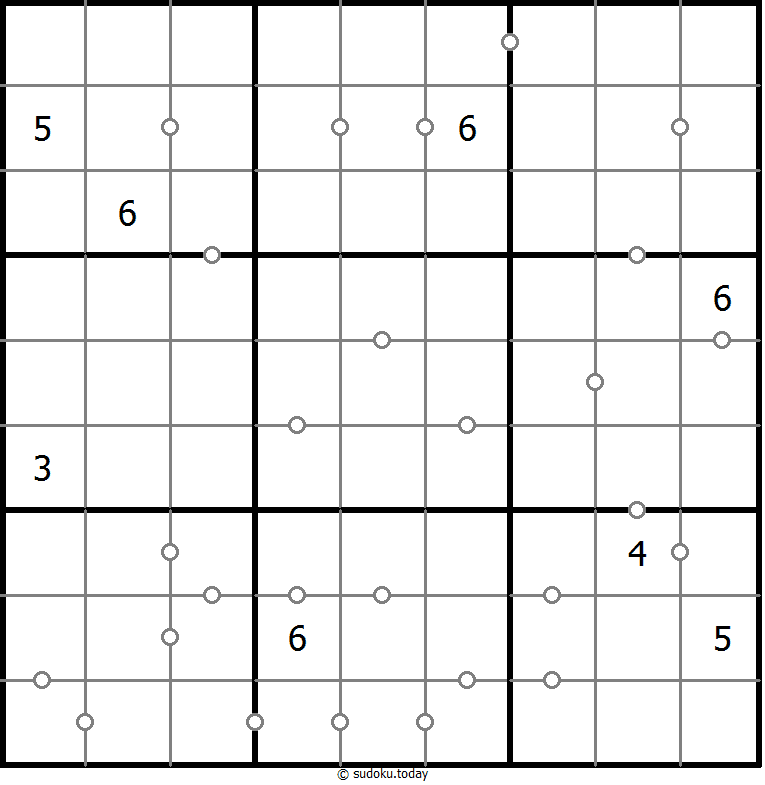
Consecutive Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. All possible dots are marked.
Thermo Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Some thermometer shapes are placed in the grid. Digits are strictly increasing from the round bulb of the thermometer to each flat end.
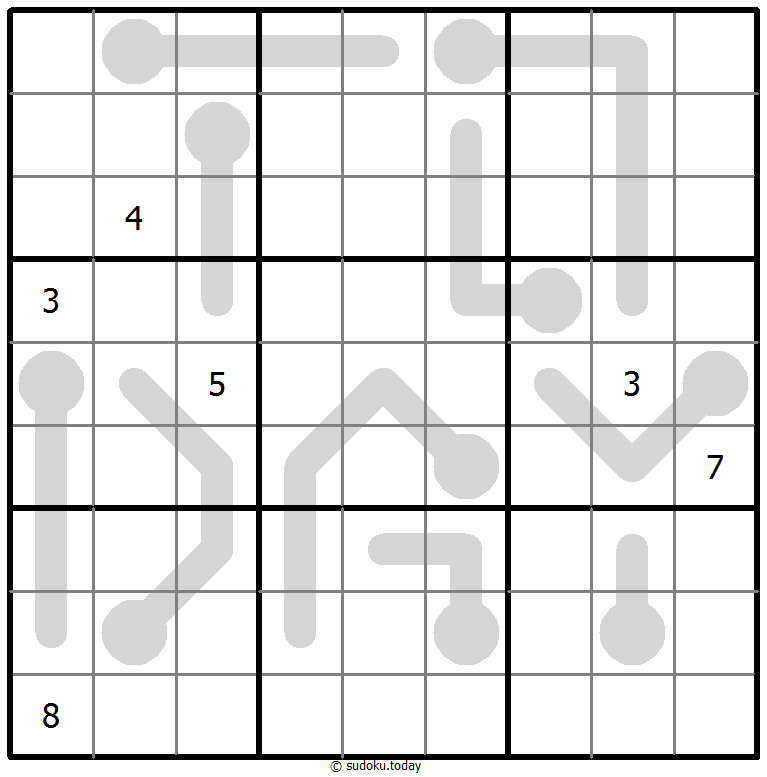
Thermo Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Some thermometer shapes are placed in the grid. Digits are strictly increasing from the round bulb of the thermometer to each flat end.
Neighbourship Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A number in a squared cell indicates how many different numbers the four diagonally adjacent cells contain. A number in a circled cell indicates how many different numbers the eight orthogonally and diagonally adjacent cells contain.
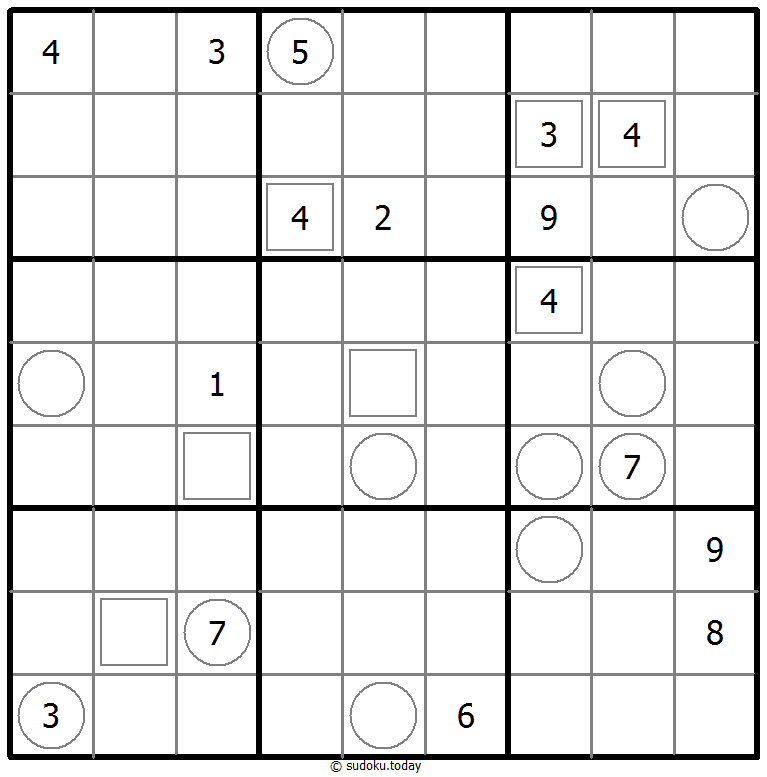
Neighbourship Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A number in a squared cell indicates how many different numbers the four diagonally adjacent cells contain. A number in a circled cell indicates how many different numbers the eight orthogonally and diagonally adjacent cells contain.
Mirror Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The four corner boxes contain the same digit in symmetric positions about the centre.
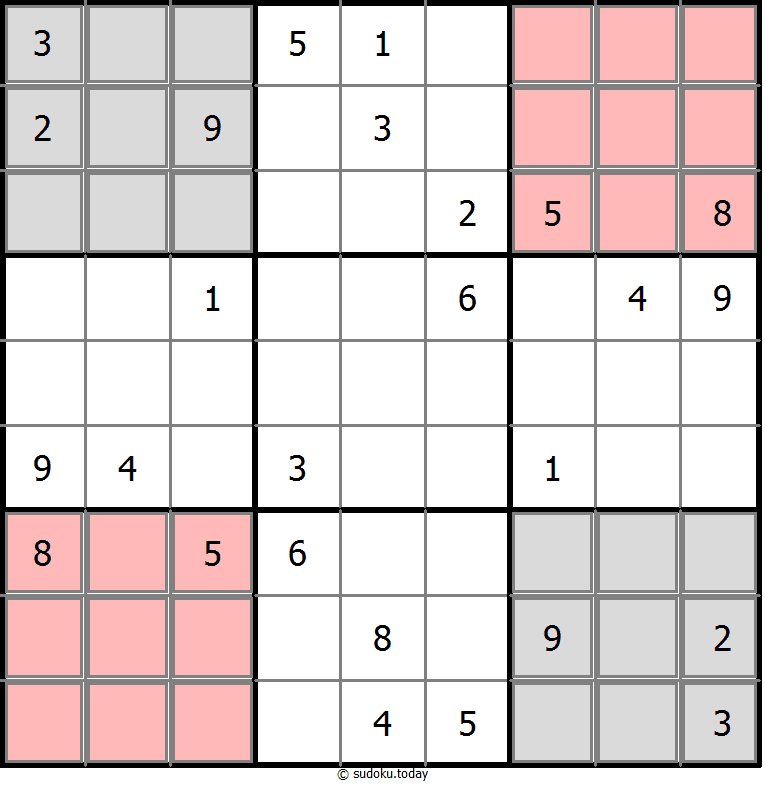
Mirror Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The four corner boxes contain the same digit in symmetric positions about the centre.
147 Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Cells with circles must contain digits 1-2-3, cells with squares must contain digits 4-5-6, blank cells must contains digits 7-8-9.
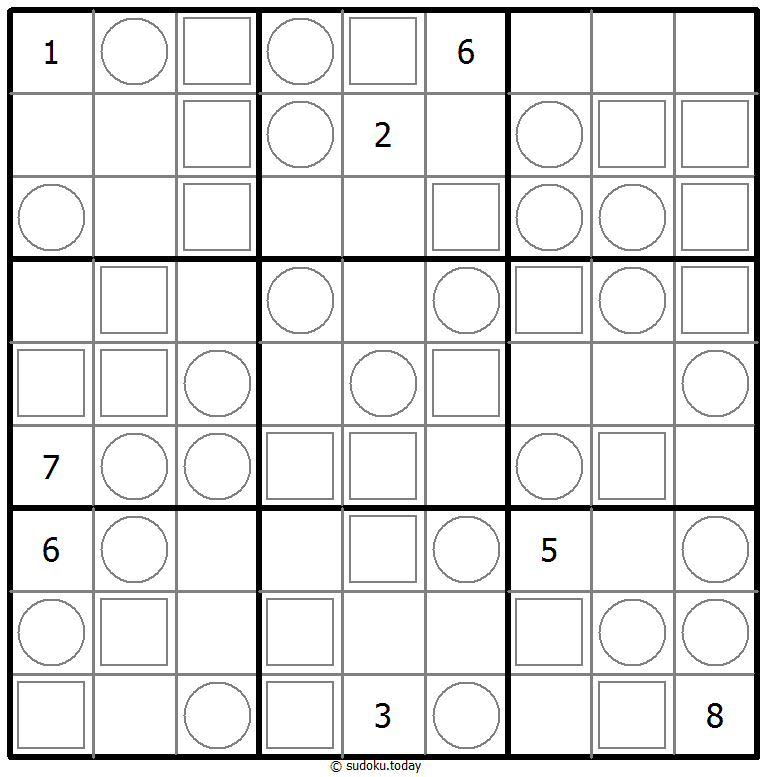
147 Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Cells with circles must contain digits 1-2-3, cells with squares must contain digits 4-5-6, blank cells must contains digits 7-8-9.
Eliminate Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The number in a cell with an arrow must not be repeated in a cell the arrow points to.
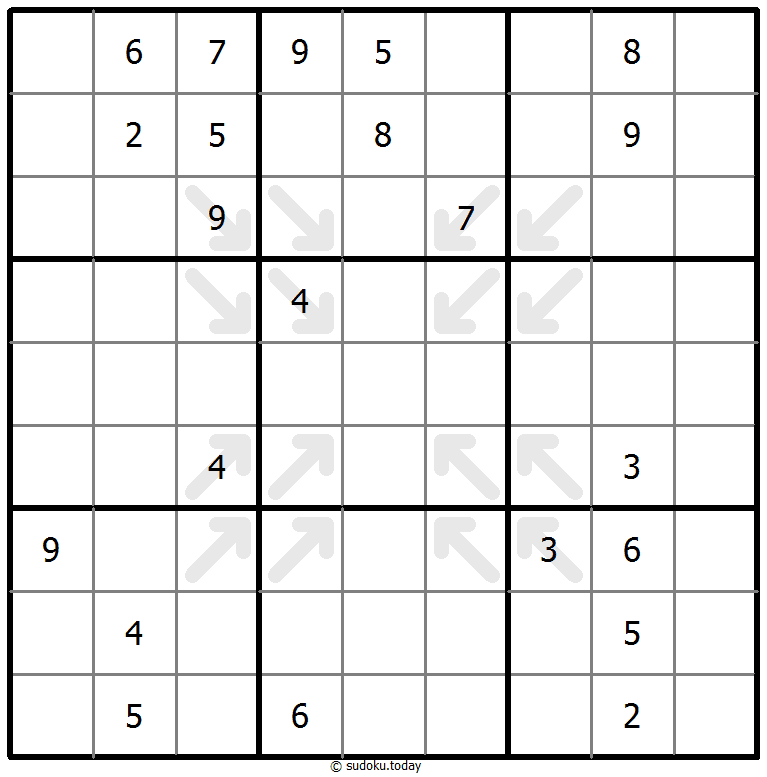
Eliminate Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The number in a cell with an arrow must not be repeated in a cell the arrow points to.
Perfect Squares
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A dot between two cells indicates that the digits in the two cells form a double digit square number in the reading direction. there are no square numbers marked by a dot.
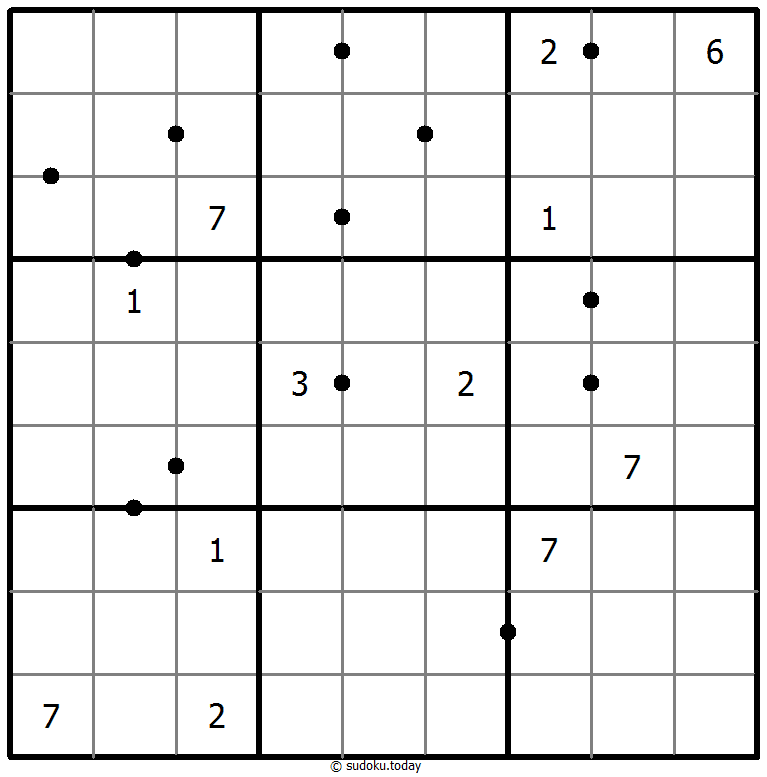
Perfect Squares
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A dot between two cells indicates that the digits in the two cells form a double digit square number in the reading direction. there are no square numbers marked by a dot.
147 Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Cells with circles must contain digits 1-2-3, cells with squares must contain digits 4-5-6, blank cells must contains digits 7-8-9.
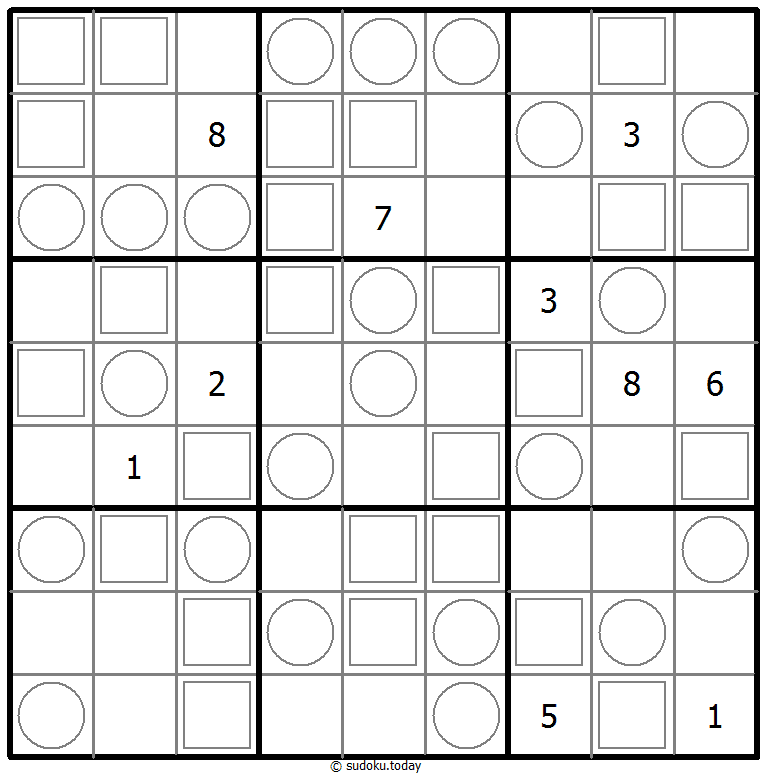
147 Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Cells with circles must contain digits 1-2-3, cells with squares must contain digits 4-5-6, blank cells must contains digits 7-8-9.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
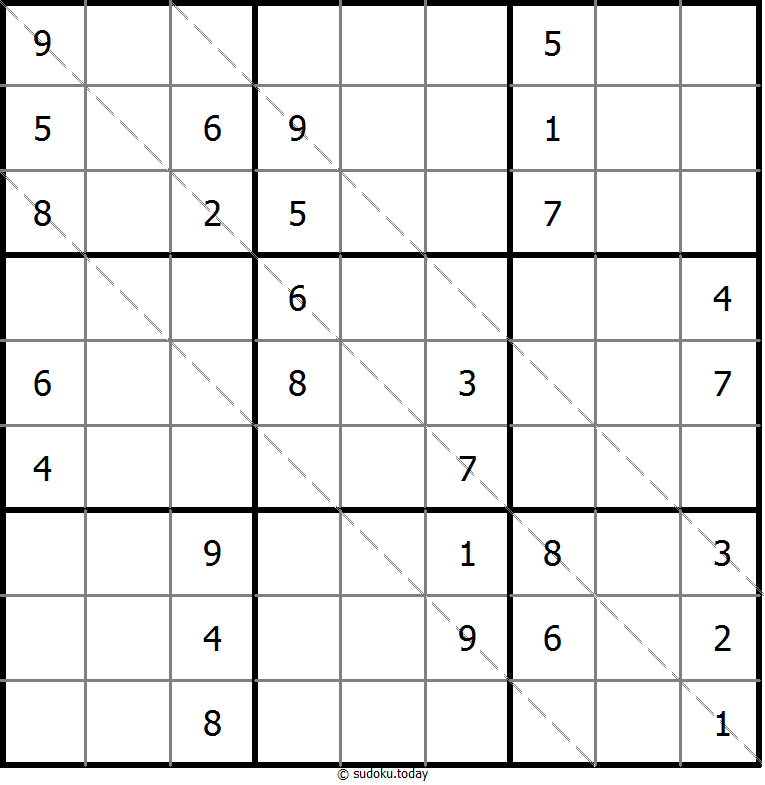
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Hybrid Sudoku ( Consecutive Pairs + Sum Frame )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
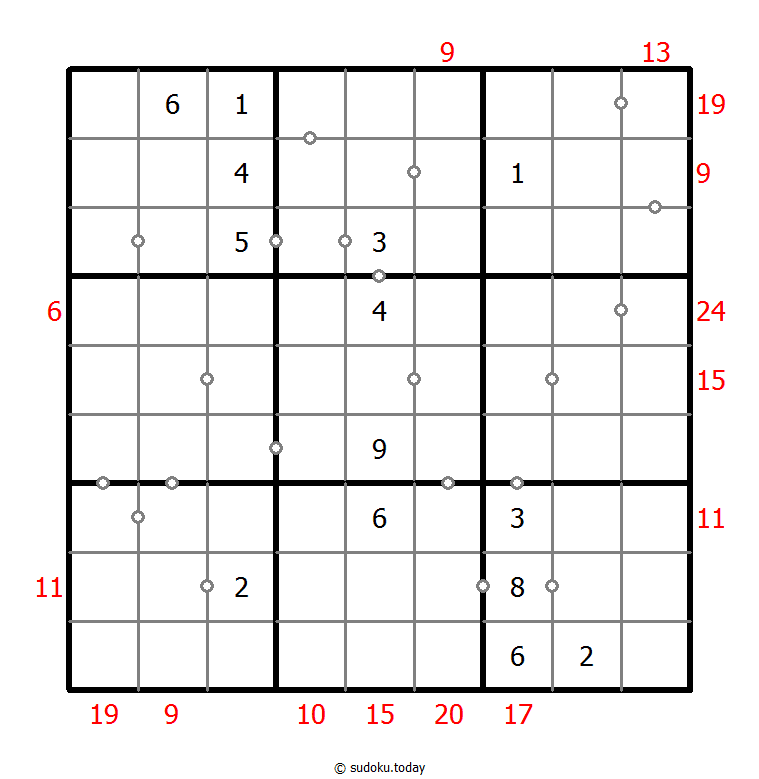
Hybrid Sudoku ( Consecutive Pairs + Sum Frame )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
Sum Frame Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
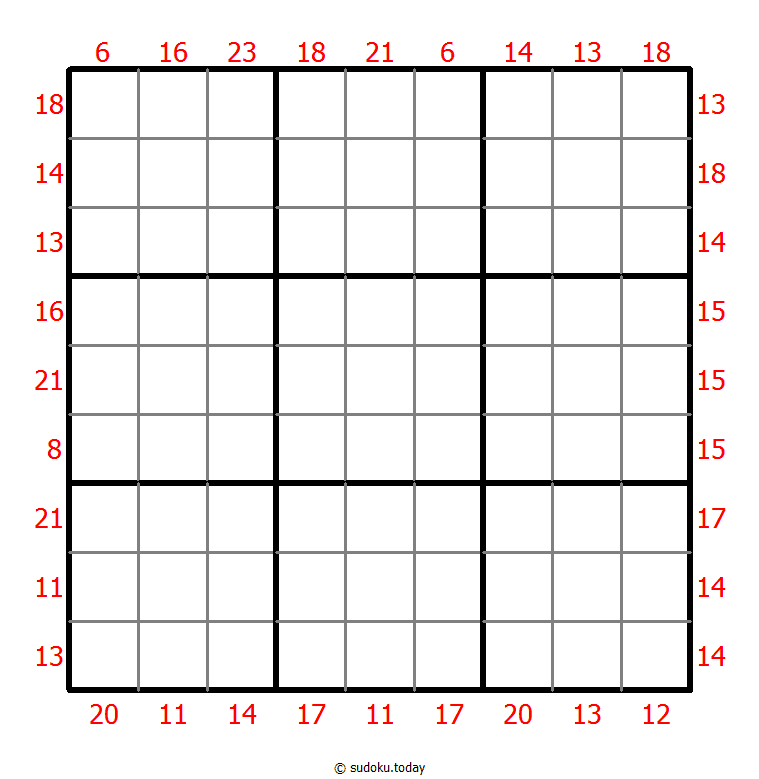
Sum Frame Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
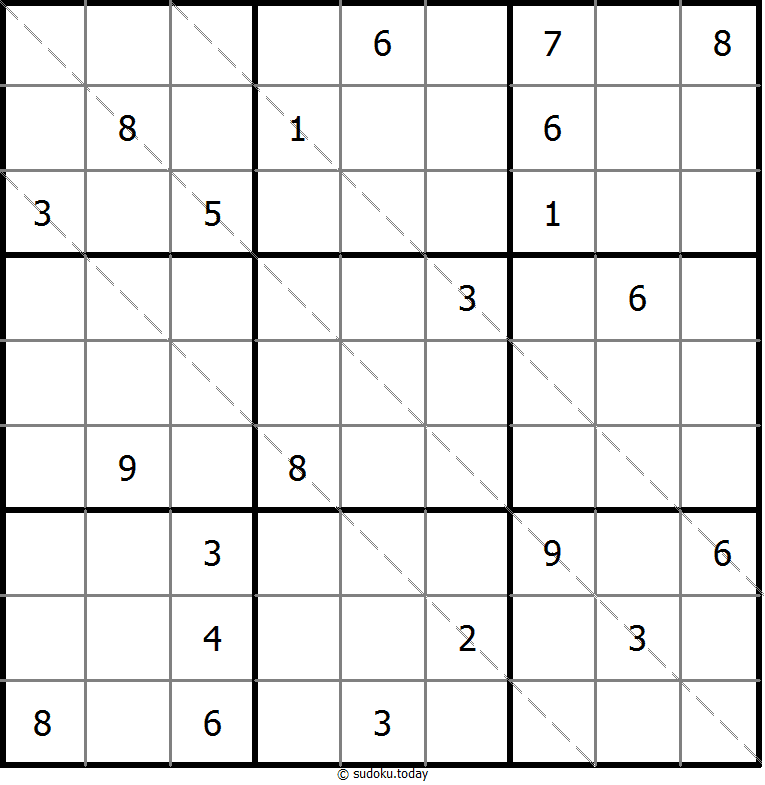
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Skyscrapers Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Consider each number to be the height of a building. The numbers outside the grid indicate how many buildings can be seen when looking in that direction (taller buildings conceal smaller buildings behind them).

Skyscrapers Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Consider each number to be the height of a building. The numbers outside the grid indicate how many buildings can be seen when looking in that direction (taller buildings conceal smaller buildings behind them).
X Sums Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
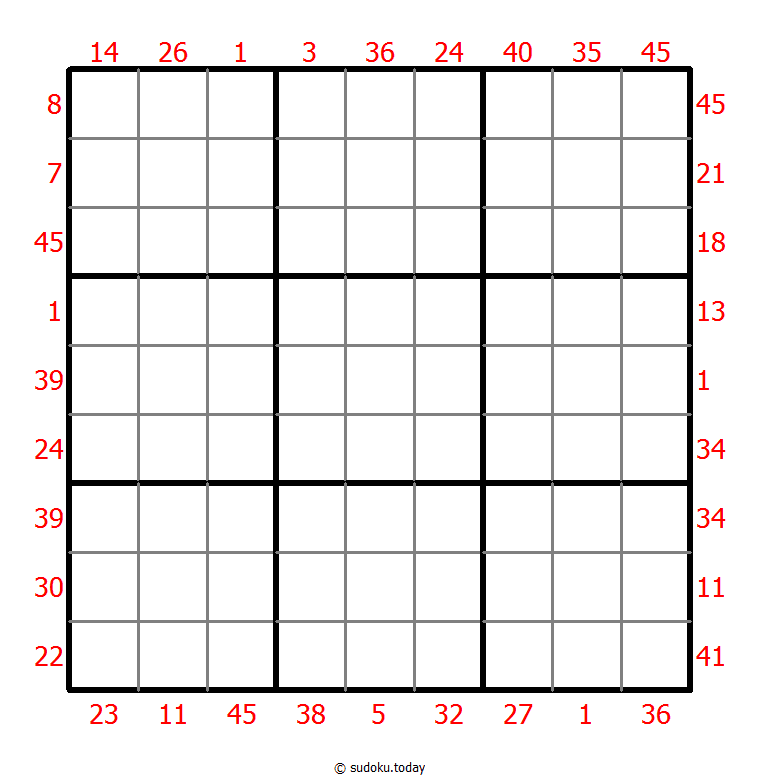
X Sums Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
Hybrid Sudoku ( Greater Than + Sum Frame )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits have to be place in accordance with the “greater than” signs.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
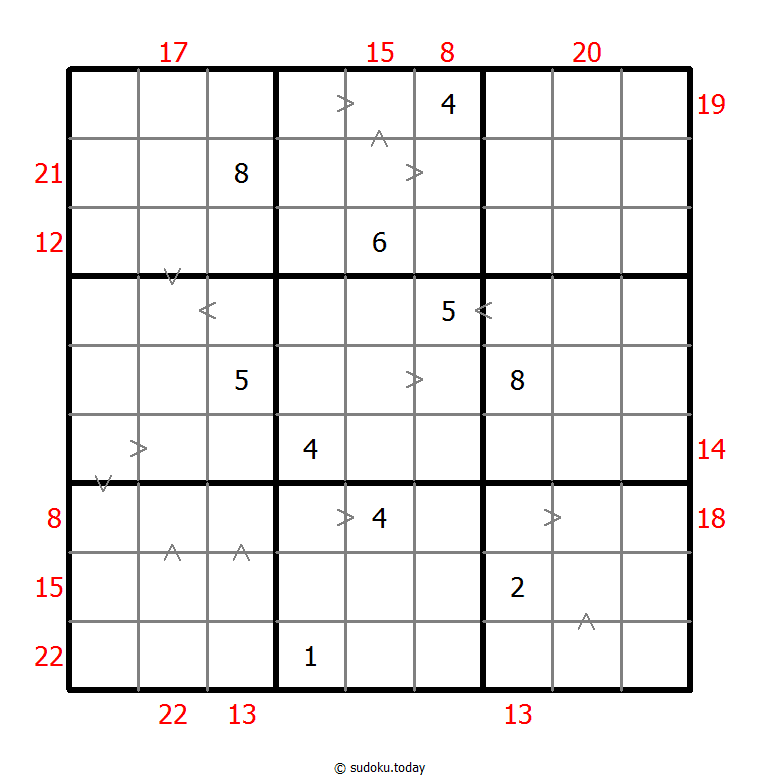
Hybrid Sudoku ( Greater Than + Sum Frame )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits have to be place in accordance with the “greater than” signs.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.

Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.
Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.

Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.
English | 中文(简体) | 中文(繁體) | 日本語 | 한국어 | Français | Deutsch | Español | Português | Русский | Italiano | Nederlands | Türkçe | हिन्दी | ไทย | Tiếng Việt | Bahasa Indonesia | Polski | Українська |
数独 | Cool Sudoku | 数独 | Sudoku Puzzle | 賢くなるパズル
© sudoku.today All rights reserved 2019-2026

