Sudokus that no one can solve
Sudokus that no one can solve, not only including very difficult ones but also puzzles that no one has attempted yet.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
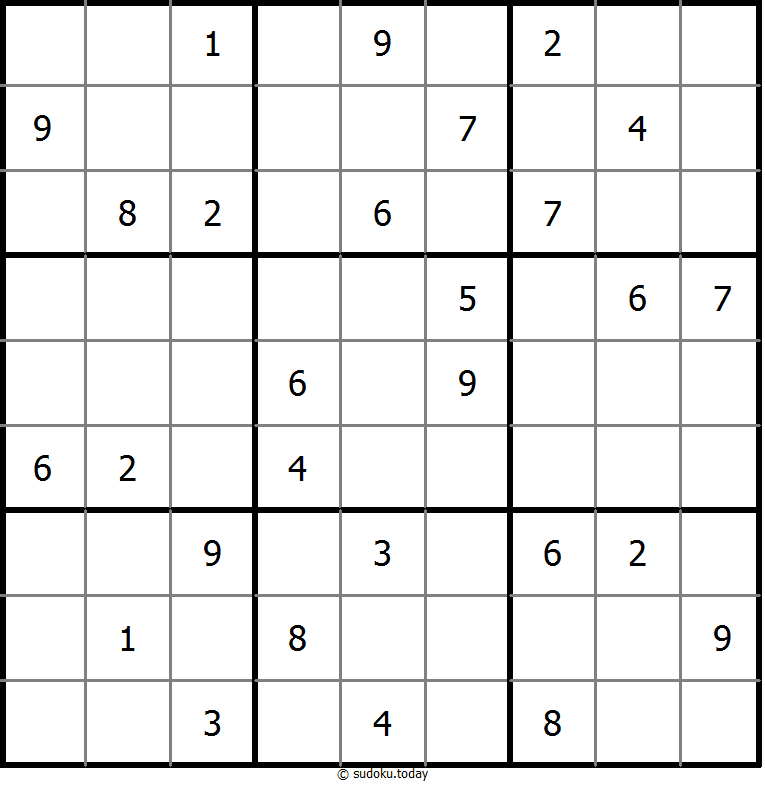
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
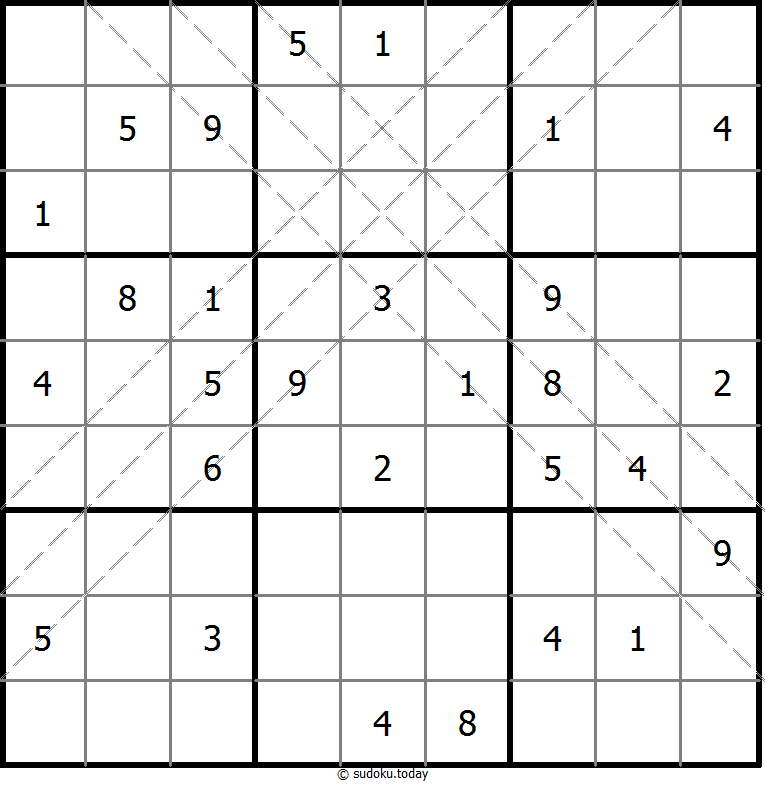
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Anti Knight Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The same numbers are not chess-knight move connected.
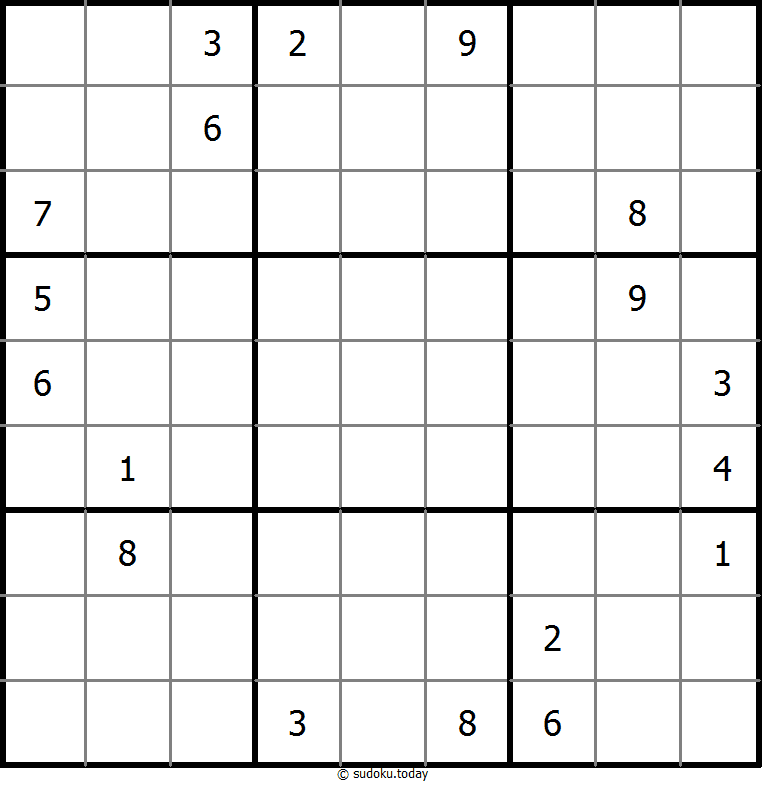
Anti Knight Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The same numbers are not chess-knight move connected.
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
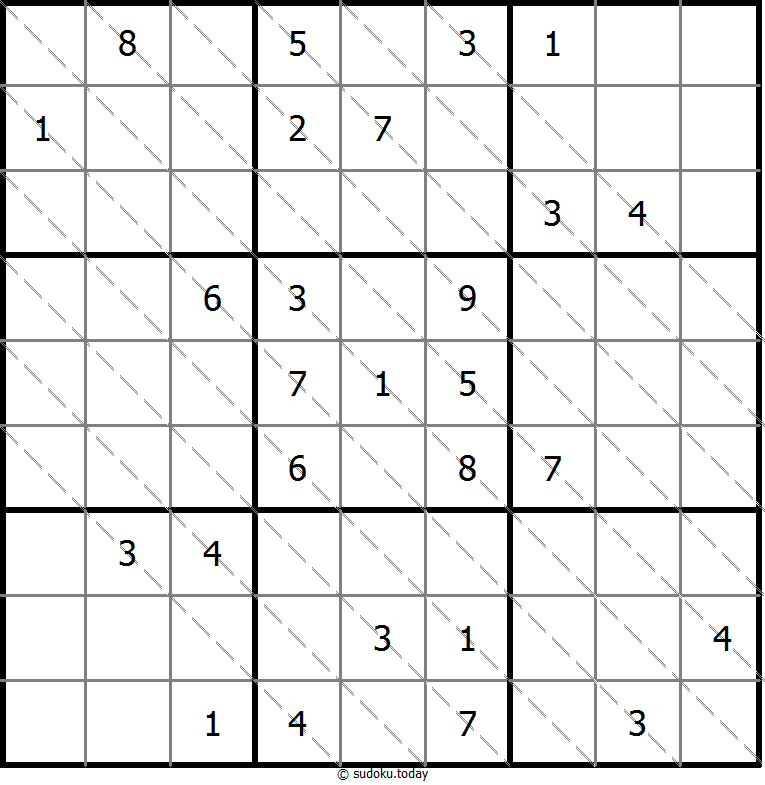
Multi Diagonal Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits do not repeat along the marked diagonals.
Clone Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Grey cells in the grid represent many cloned areas. Digits in these areas on corresponding positions must be identical. Cloned areas are only moved, without rotation or reflection.
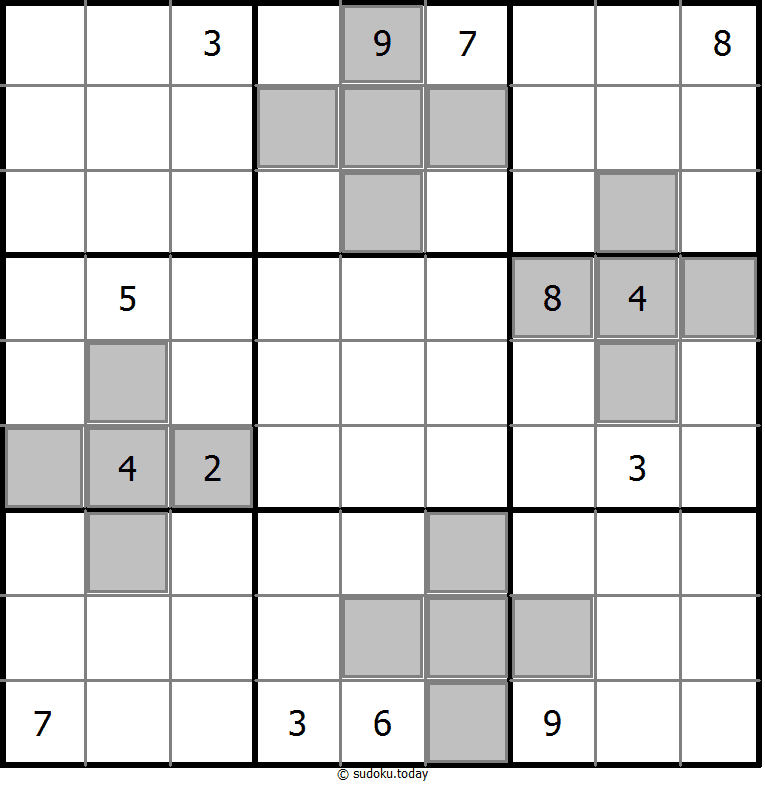
Clone Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Grey cells in the grid represent many cloned areas. Digits in these areas on corresponding positions must be identical. Cloned areas are only moved, without rotation or reflection.
Consecutive Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.

Consecutive Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.
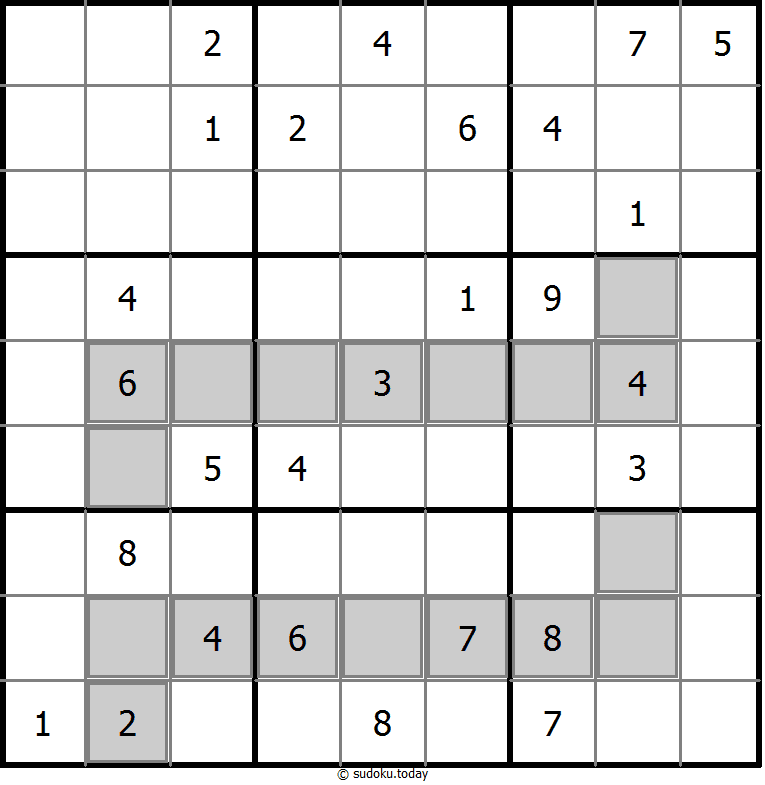
Extra Regions Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The connected shaded cells contain each digit from 1 to 9.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
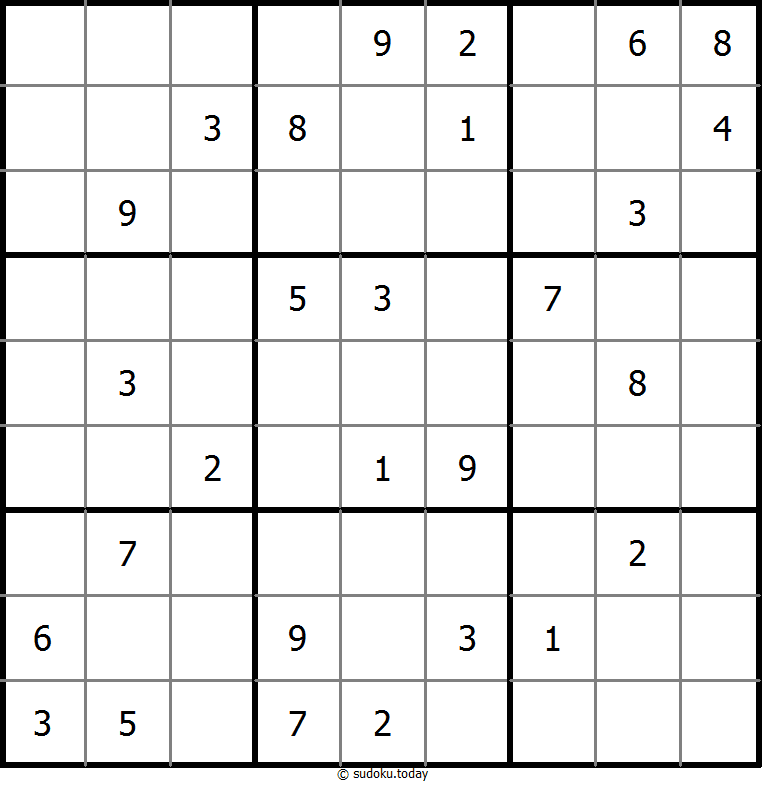
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
No Touch Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Identical digits do not touch each other diagonally.
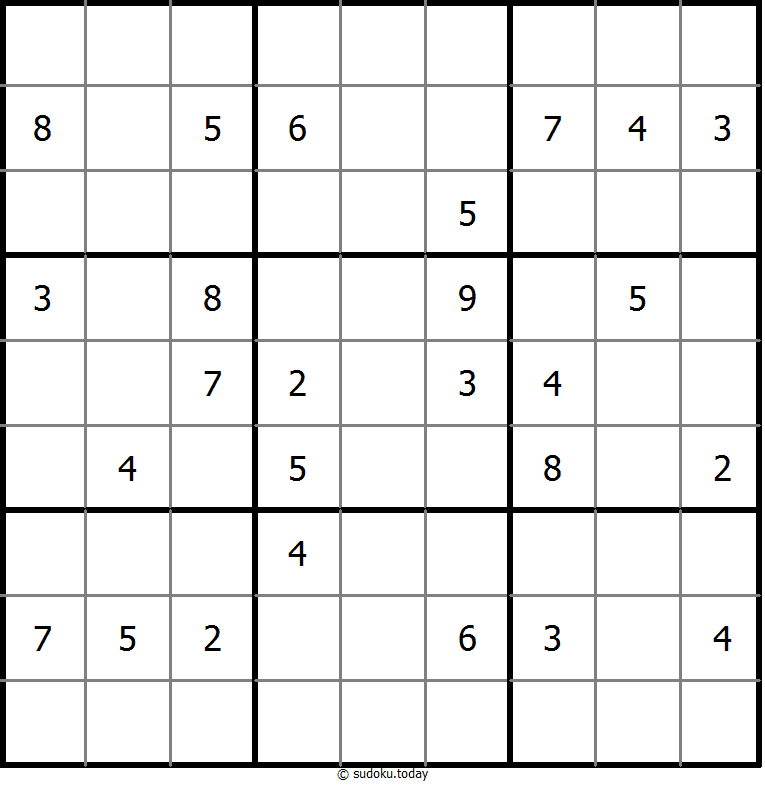
No Touch Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Identical digits do not touch each other diagonally.
Sum Frame Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
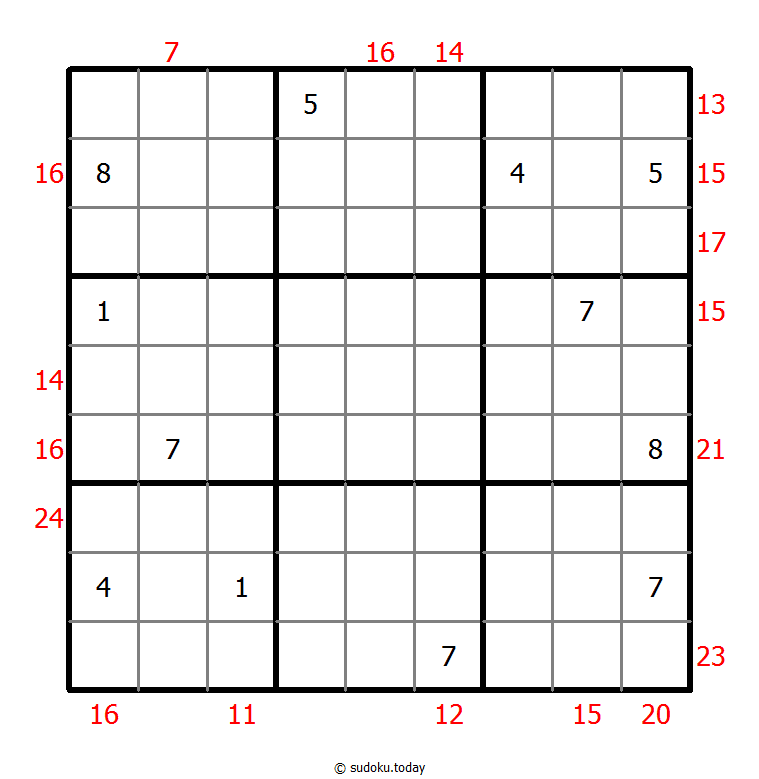
Sum Frame Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits outside the grid indicate the sum of the first 3 digits in the corresponding direction.
Hybrid Sudoku ( X Sums + Consecutive )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
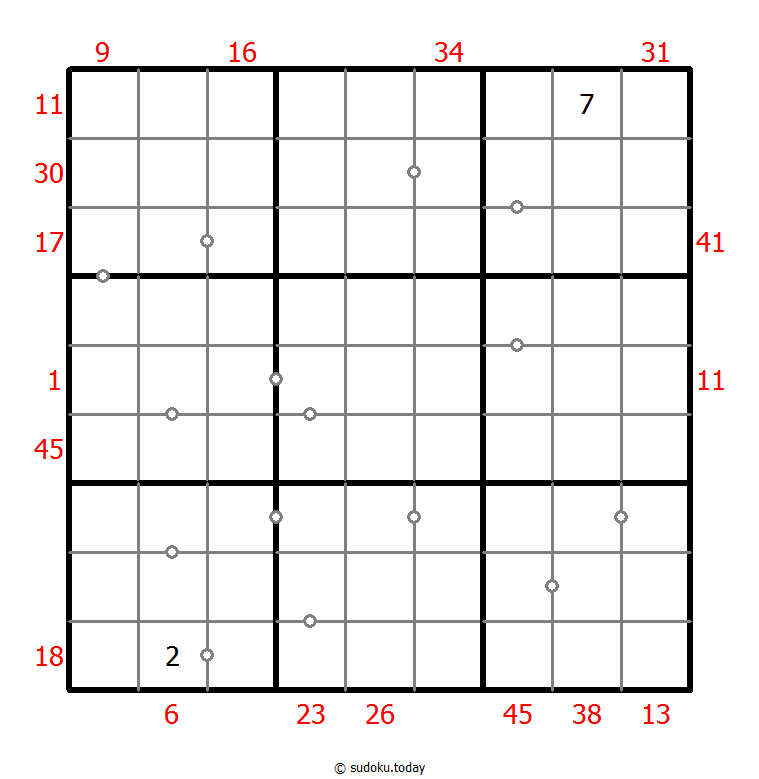
Hybrid Sudoku ( X Sums + Consecutive )
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Each number outside the grid is the sum of the first X numbers placed in the corresponding direction, where X is equal to the first number placed in that direction.
- There are some dots between cells. The numbers on each side of a dot must always be consecutive. Not all possible dots are marked.
Rossini Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The arrows outside the grid indicate that the nearest three digits in the corresponding direction are in ascending or descending order (the highest number is always in the direction of the arrow). All possible arrows are given, so if there is no arrow, the first three digits do not form an increasing sequence in either direction.
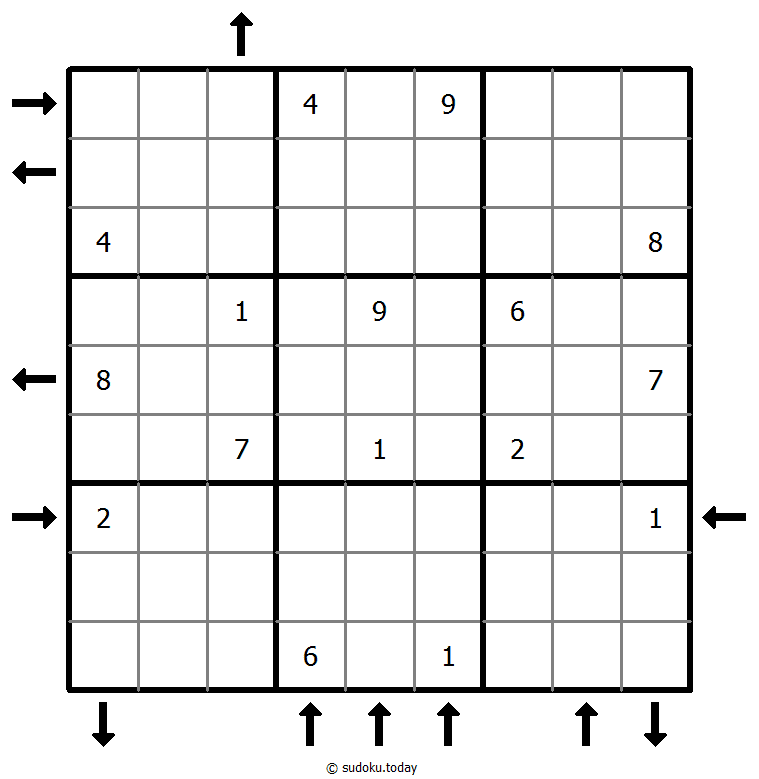
Rossini Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- The arrows outside the grid indicate that the nearest three digits in the corresponding direction are in ascending or descending order (the highest number is always in the direction of the arrow). All possible arrows are given, so if there is no arrow, the first three digits do not form an increasing sequence in either direction.
Skyscrapers Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Consider each number to be the height of a building. The numbers outside the grid indicate how many buildings can be seen when looking in that direction (taller buildings conceal smaller buildings behind them).
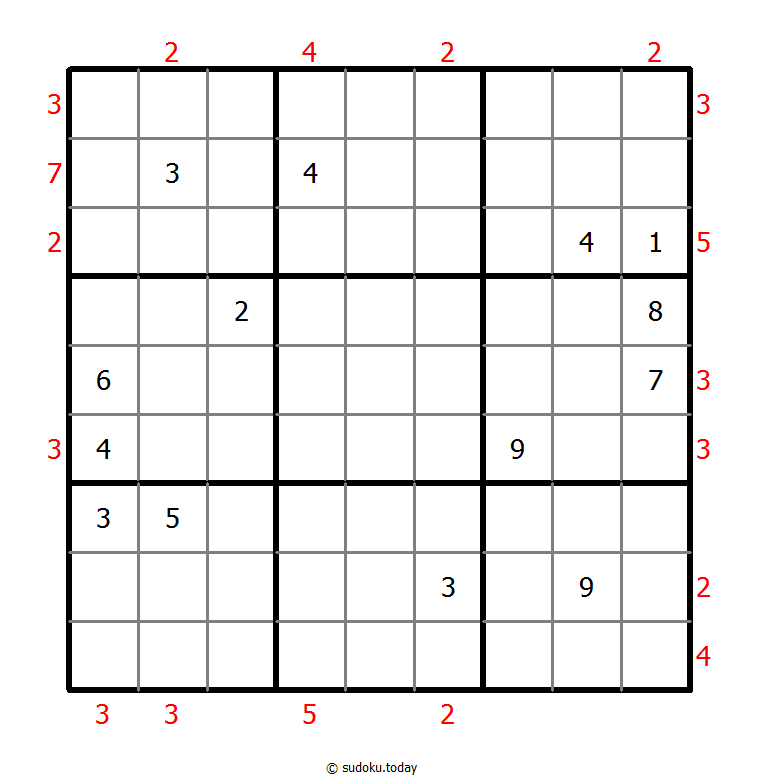
Skyscrapers Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Consider each number to be the height of a building. The numbers outside the grid indicate how many buildings can be seen when looking in that direction (taller buildings conceal smaller buildings behind them).
Sujiken
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Sujiken (from Japanese "sujikai", literally "diagonal") is a variation of Sudoku . The puzzle consists of a triangular grid of cells containing digits from 1 to 9. The objective is to fill a grid with digits so that each cell contains a digit and no digit is repeated in any column, row and diagonal in any direction. Also, no digit occurs twice in any of the three larger 3 x 3 square regions and any of the three larger triangular regions enclosed by thick borders.
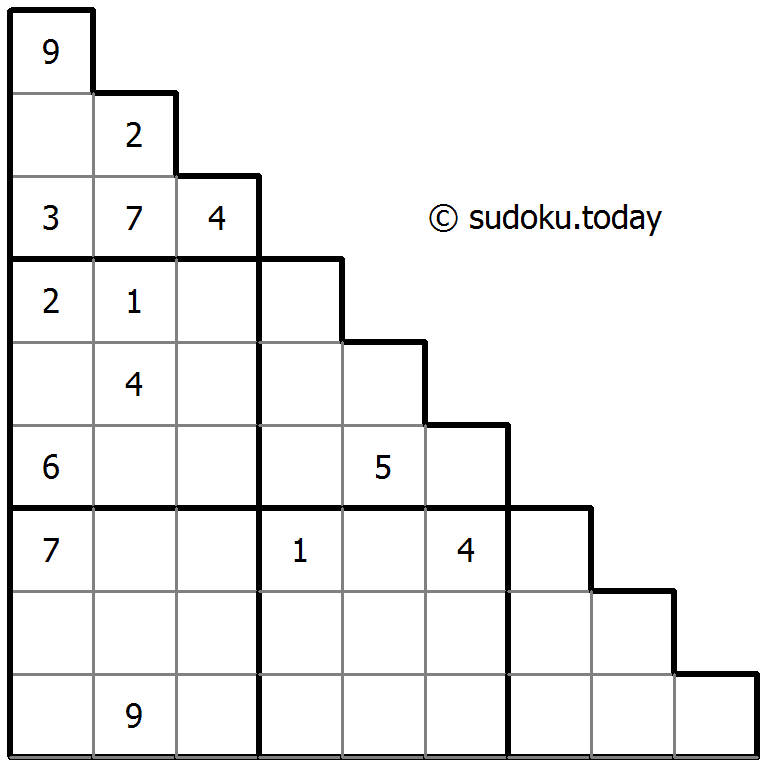
Sujiken
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Sujiken (from Japanese "sujikai", literally "diagonal") is a variation of Sudoku . The puzzle consists of a triangular grid of cells containing digits from 1 to 9. The objective is to fill a grid with digits so that each cell contains a digit and no digit is repeated in any column, row and diagonal in any direction. Also, no digit occurs twice in any of the three larger 3 x 3 square regions and any of the three larger triangular regions enclosed by thick borders.
Answer 8 sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A dot between two cells indicates that the result of at least one of the basic operations (addition, subtraction, multiplication, division) of the numbers in these two cells is 8. Is the dot missing, no one of the basic operations results in an 8.
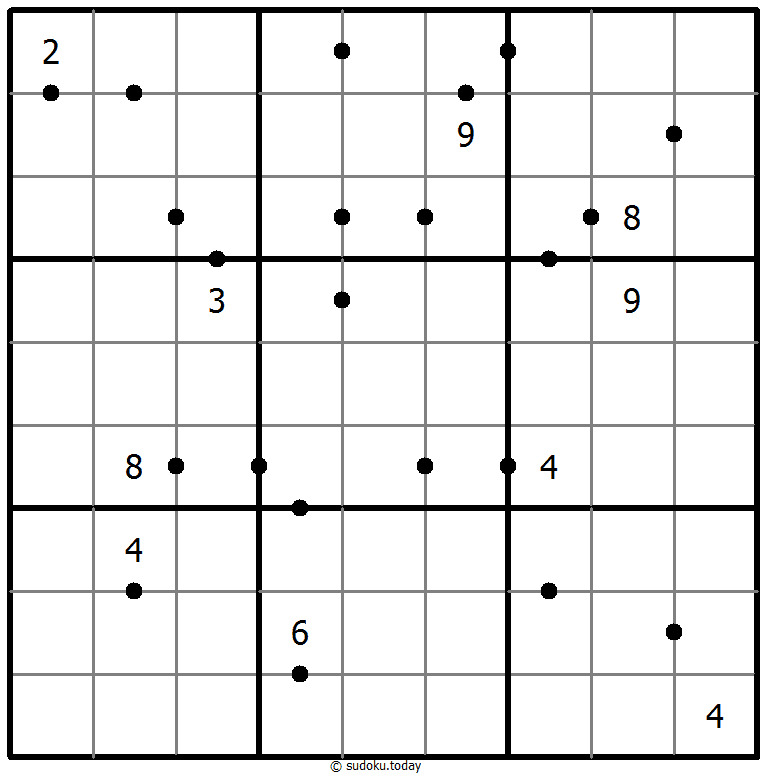
Answer 8 sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A dot between two cells indicates that the result of at least one of the basic operations (addition, subtraction, multiplication, division) of the numbers in these two cells is 8. Is the dot missing, no one of the basic operations results in an 8.
Products Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A number between two cells indicates the product of the numbers in these cells. A number between four cells indicates the product between two diagonally adjacent cells, either top left + right bottom (\) or top right + bottom left (/).
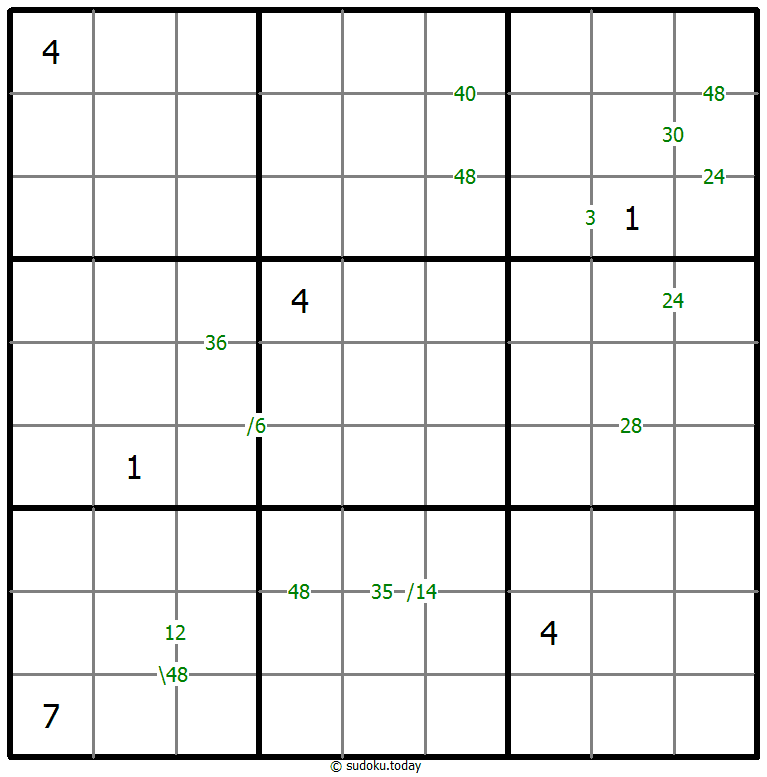
Products Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- A number between two cells indicates the product of the numbers in these cells. A number between four cells indicates the product between two diagonally adjacent cells, either top left + right bottom (\) or top right + bottom left (/).
Quad Sums Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- One of the numbers in the four cells around a dot is the num of the other three numbers.
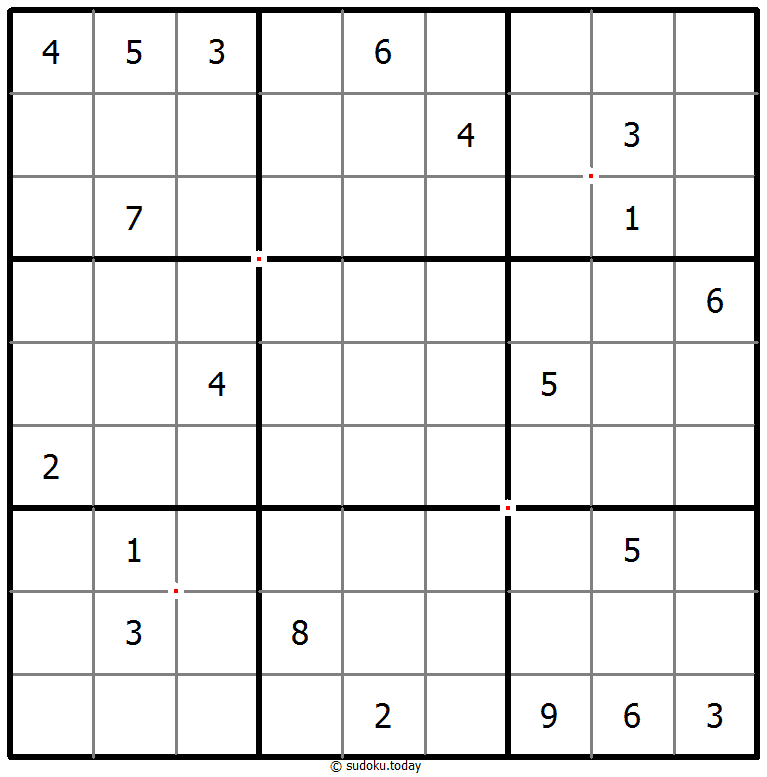
Quad Sums Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- One of the numbers in the four cells around a dot is the num of the other three numbers.
Mathrax Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Some intersections of the grid lines are marked by a number and an operator (+, -, x, /) in a circle. The number is the result of the operation, applied to both pairs of diagonally opposite cells. An E in the circle indicates that all four adjacent digits are even, while an O indicates that all four adjacent digits are odd.
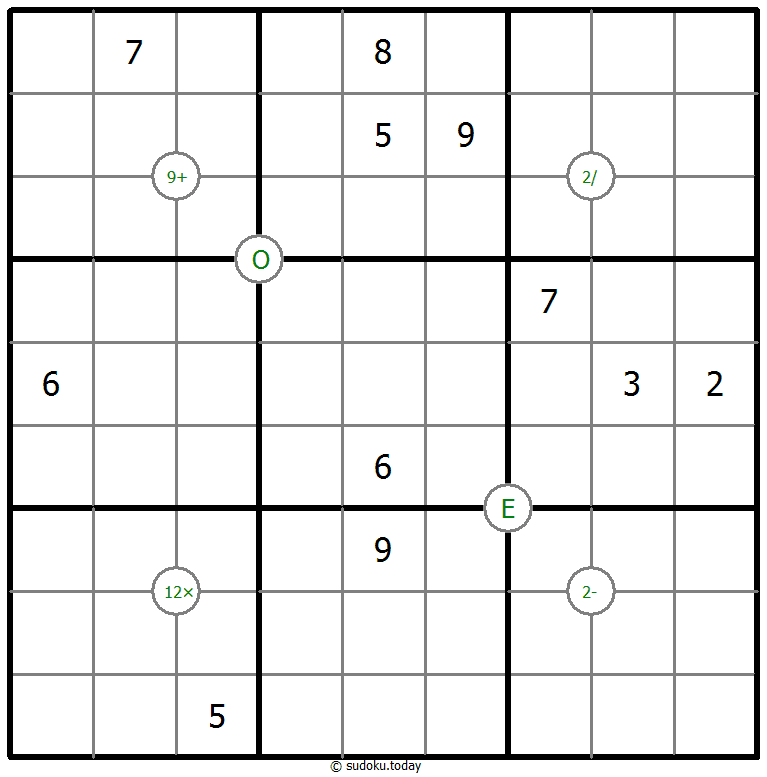
Mathrax Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Some intersections of the grid lines are marked by a number and an operator (+, -, x, /) in a circle. The number is the result of the operation, applied to both pairs of diagonally opposite cells. An E in the circle indicates that all four adjacent digits are even, while an O indicates that all four adjacent digits are odd.
Battenburg Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Everywhere 2 odd and 2 even digits form a 2x2 checkerboard pattern, a Battenburg marking is given. A checkerboard pattern is a 2x2 area of cells where the top-left and bottom-right cells are of one type and the top-right and bottom-left cells are of another type. All possible dots are marked.
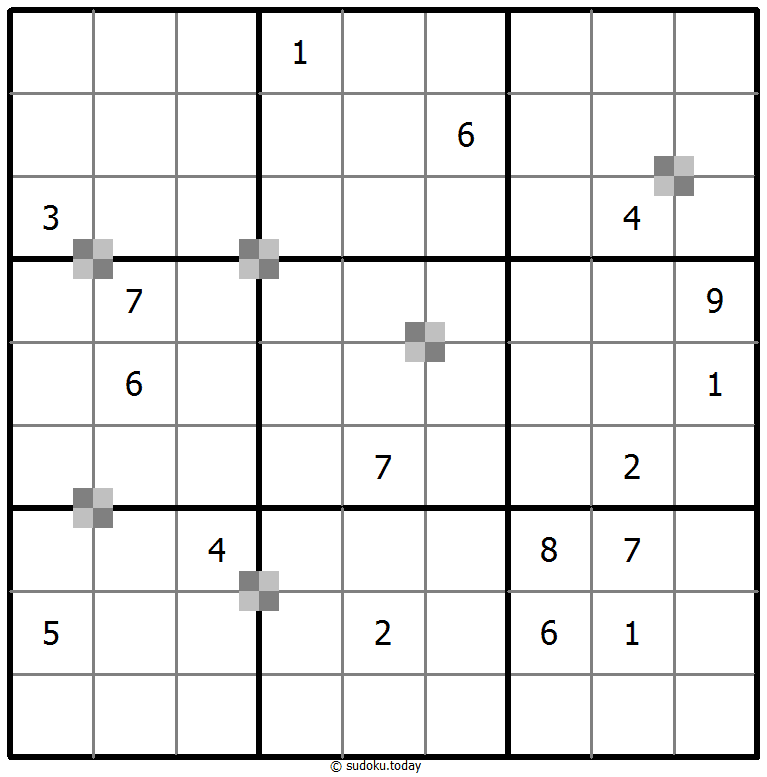
Battenburg Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Everywhere 2 odd and 2 even digits form a 2x2 checkerboard pattern, a Battenburg marking is given. A checkerboard pattern is a 2x2 area of cells where the top-left and bottom-right cells are of one type and the top-right and bottom-left cells are of another type. All possible dots are marked.
Thermo Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Some thermometer shapes are placed in the grid. Digits are strictly increasing from the round bulb of the thermometer to each flat end.
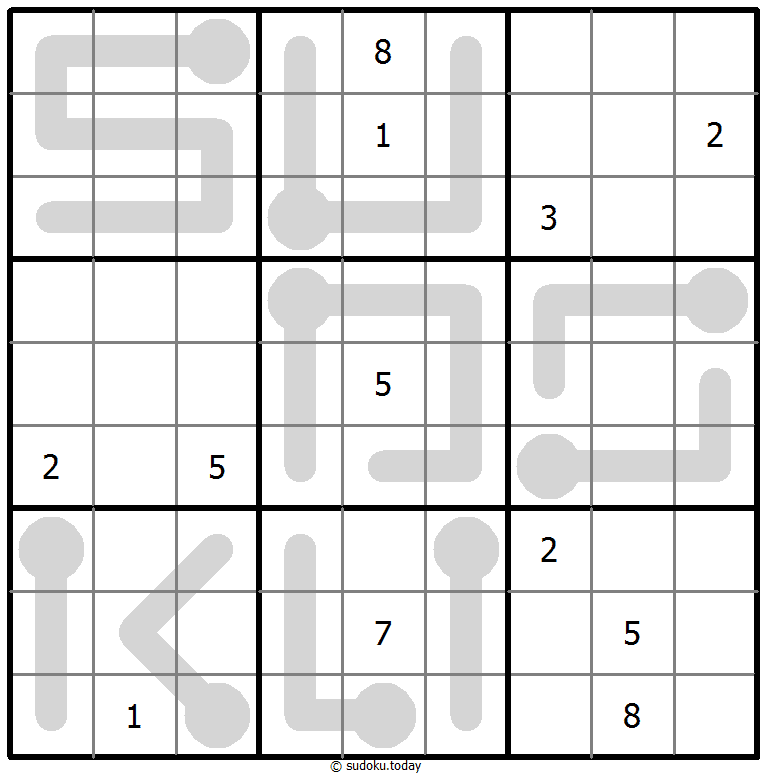
Thermo Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Some thermometer shapes are placed in the grid. Digits are strictly increasing from the round bulb of the thermometer to each flat end.
Parity Lines Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits along each marked line are either all odd or all even.
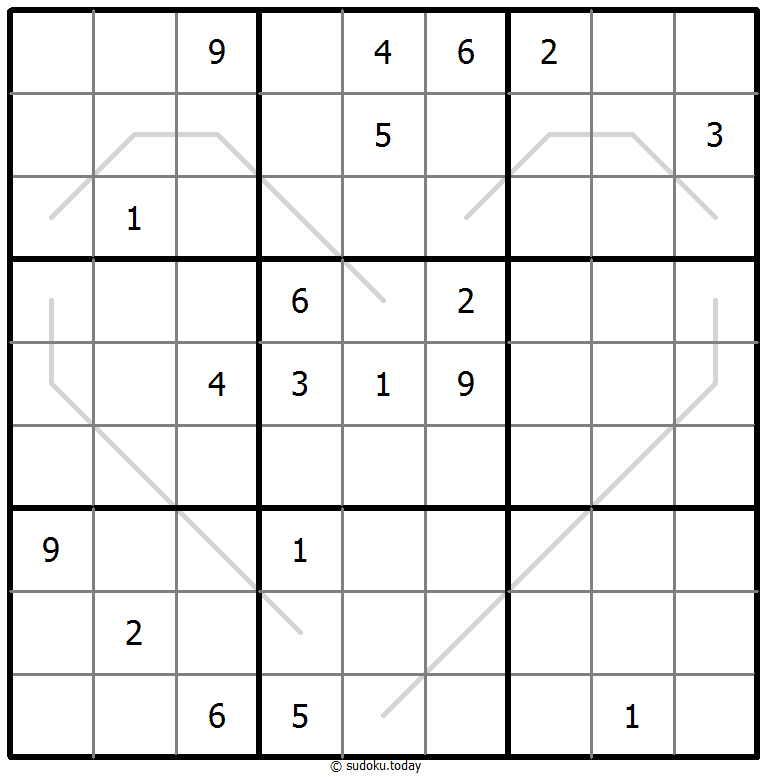
Parity Lines Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
- Digits along each marked line are either all odd or all even.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.

Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
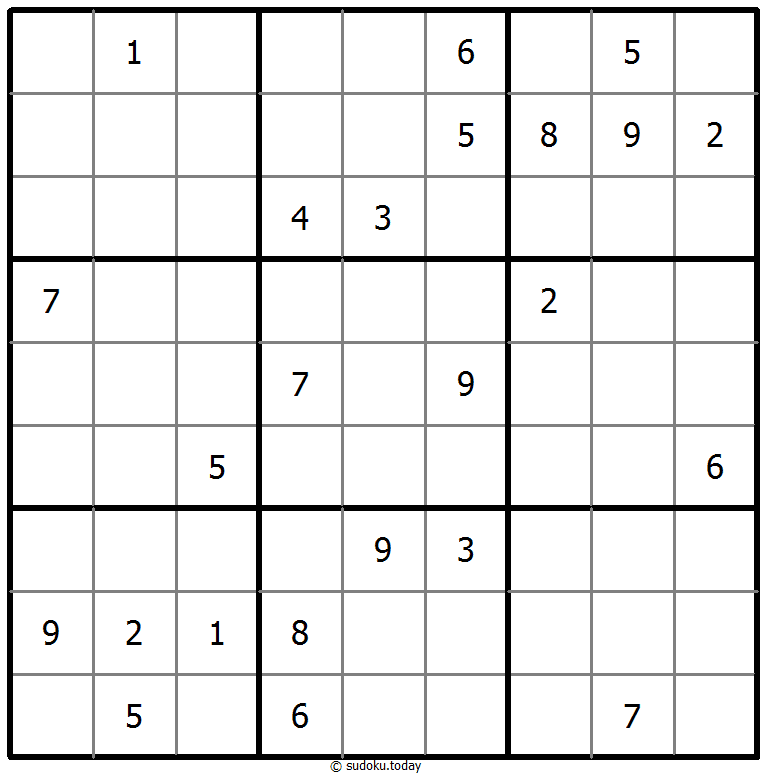
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
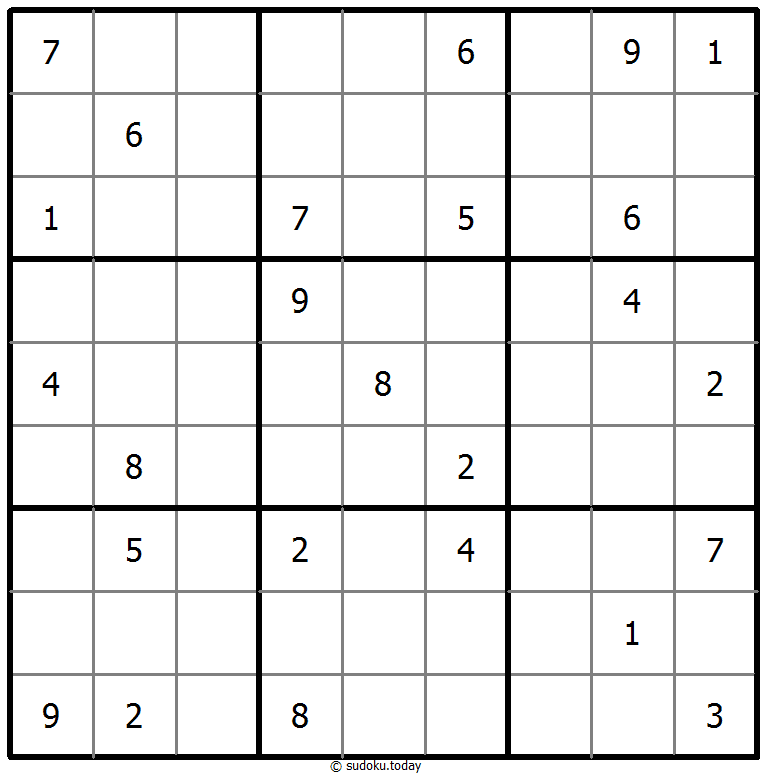
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
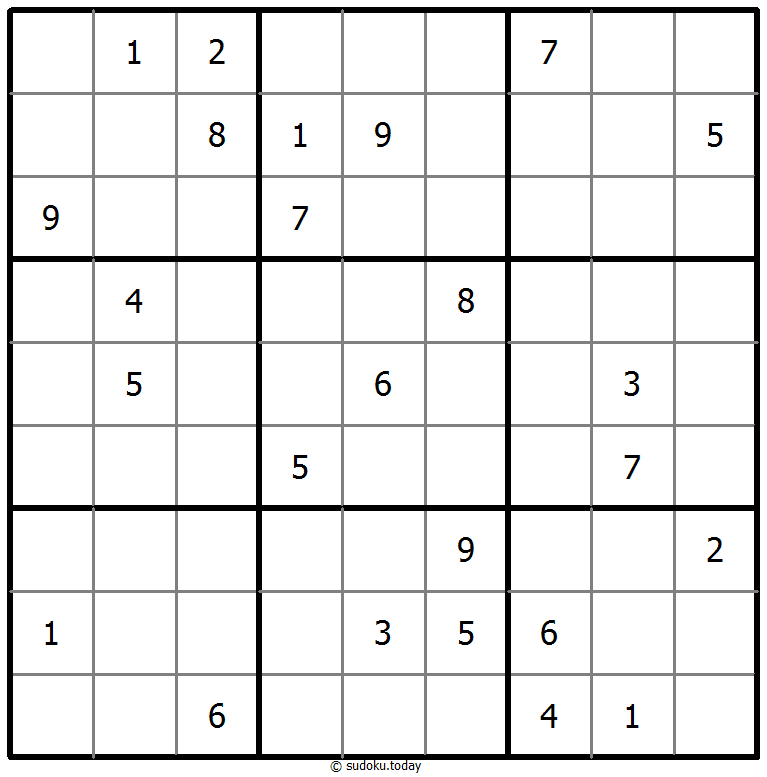
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
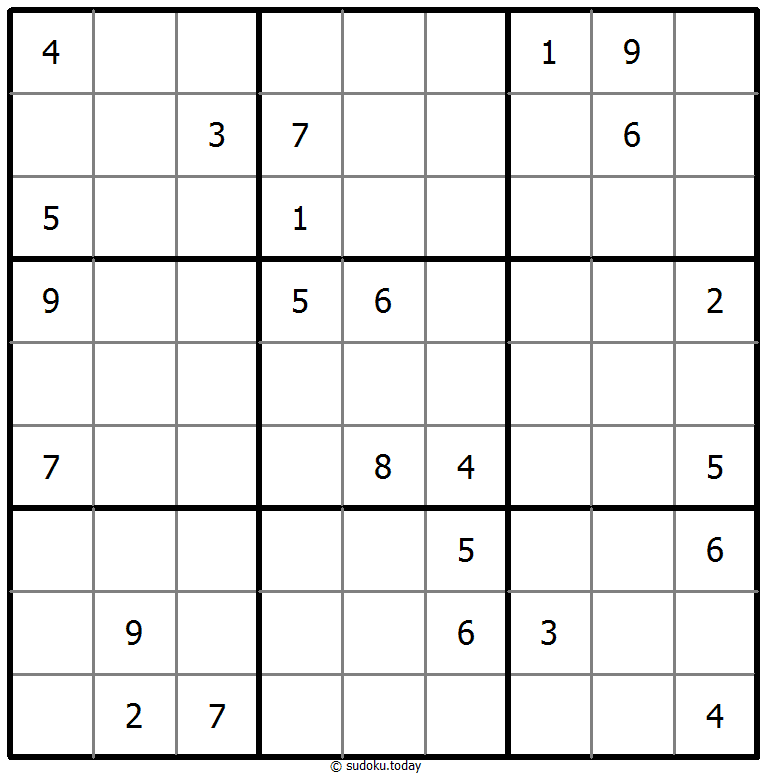
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
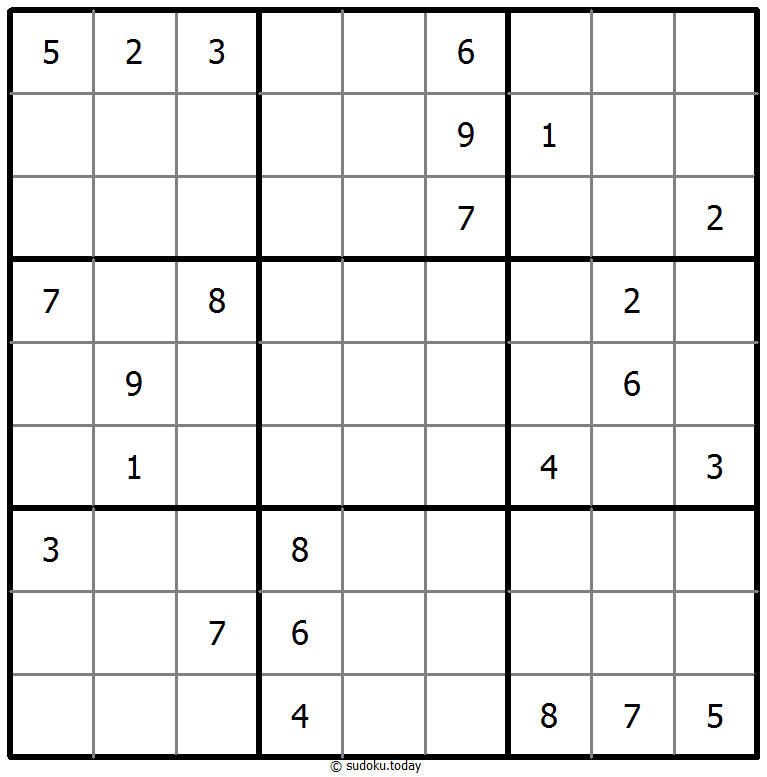
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
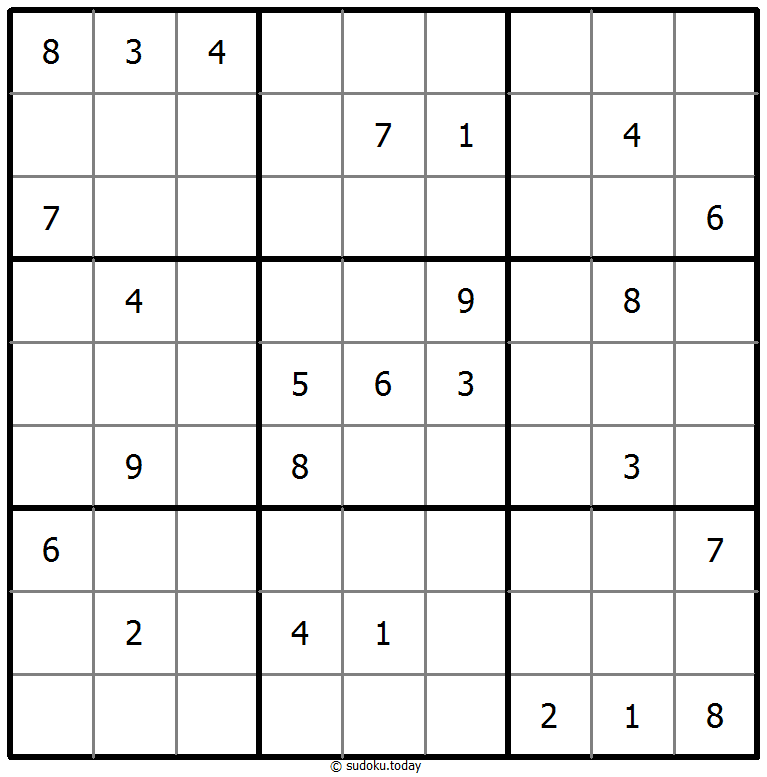
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
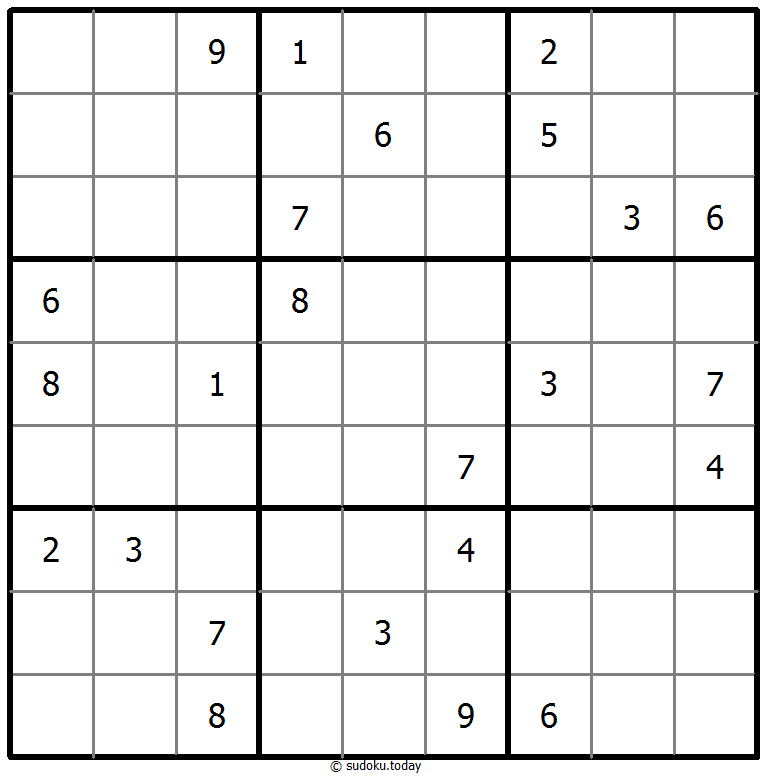
Classic Sudoku
- Place a digit from 1 to 9 into each of the empty squares so that each digit appears exactly once in each of the rows, columns and the nine outlined 3x3 regions.
English | 中文(简体) | 中文(繁體) | 日本語 | 한국어 | Français | Deutsch | Español | Português | Русский | Italiano | Nederlands | Türkçe | हिन्दी | ไทย | Tiếng Việt | Bahasa Indonesia | Polski | Українська |
数独 | Cool Sudoku | 数独 | Sudoku Puzzle | 賢くなるパズル
© sudoku.today All rights reserved 2019-2026
